Continuity of a Function

Find the value of $p$ and $q$ for which the function

$f\left(x\right)=\left\{\begin{array}{c}\frac{\sin \left(p+1\right)x\left(\sin x\right)}{x}, x<0\\ q x=0\\ \frac{\sqrt{x+x^2}-\sqrt{x}}{x^{{\displaystyle \frac{3}{2}}}}, x>0\end{array}\right.$

is continuous for all $x$ in $R$,

Let $g\left(x\right)$  be a polynomial of degree one and $f\left(x\right)$  be a continuous and differentiable function defined by $f\left(x\right)=\left\{\begin{array}{cc}g\left(x\right),& x\le 0\\ {\left(\frac{1+x}{2+x}\right)}^{\frac{1}{x}},& x>0\end{array}\right.$. If $f^{\text{'}}\left(1\right)=f^{\text{'}}\left(-1\right)$, then

$\text{If }\text{f}\left(x\right)=[\begin{array}{cc}x+\left\{x\right\}+x\text{sin}\left\{x\right\}& \text{for}x\ne 0\\ 0& \text{for}x=0\end{array}\text{where}\left\{x\right\}\text{denotes the fractional part function, then:}$

Choose the correct statement on the continuity of the function $f$ given by  $f\left(x\right)=\left\{\begin{array}{ll}x,& \mathrm{if} x\ge 0\\ x^2,& \mathrm{if} x<0\end{array}\right.$at $x=0$

If the function $f\left(x\right)=\left\{\begin{array}{c}\begin{array}{cc}ax+b& x<0\\ e^x& 0\le x\le 3\\ -\frac{1}{2}a& x>3\end{array}\end{array}\right.$

is continuous, then $(a, b)=$

Consider $f:(-1,1)\to \mathrm{ℝ}$ defined by $f\left(x\right)=\sqrt{x^2+x^3}.$ Then

$\underset{x\to 0^{+}}{\lim }\left[x\right]+\underset{x\to 0^{-}}{\lim }\left[x\right]$ is equal to, where $\left[·\right]$ represents greatest integer function

The number of values of $a\in \mathrm{ℝ}$ for which the function $f:\mathrm{ℝ}\to \mathrm{ℝ}$ defined by

$\left\{\begin{array}{l}\frac{\sin ax}{x}, \mathrm{if} x<0\\ a\left(x-a\right), \mathrm{if} x\ge 0 \end{array}\right.$

is continuous, is

Let $f:\mathrm{ℝ}\to \mathrm{ℝ}$ be defined by $f\left(x\right)=\left\{\begin{array}{ll}x+1,& x\ge 0\\ 0,& \text{otherwise}\end{array}\right.$ and $g\left(x\right)=x^2$. Which of the following statements is TRUE ?

If $f:\mathrm{ℝ}\to \mathrm{ℝ}$ is defined by $f\left(x\right)=\left(x-1\right)\left|x-1\right|$, then

Let the function $f:\mathrm{ℝ}\to \mathrm{ℝ}$ be defined by $f\left(x\right)=\left\{\begin{array}{ll}kx,& x\le \mathrm{\pi }\\ \cos x,& \text{otherwise}\end{array}\right.$. If $f$ is continuous at all $x\in \mathrm{ℝ}$, then $k$ is equal to

Let $f:\left[0,2\right]\to \mathrm{ℝ}$ be defined by $f\left(x\right)=\left[x\right]-\left[x+\frac{1}{2}\right]$, where $\left[x\right]$ denotes the greatest integer less than equal to $x$. At how many points of $\left[0,2\right]$, is $f$ discontinuous ?

An example of a function which is continuous but not differentiable is

Consider the function $f\left(x\right)={\left(x-1\right)}^{\frac{1}{2-x}}$. The value of $f\left(2\right)$ so that $f$ is continuous at $x=2$ is -

Function $f\left(x\right)=\cos \left(\frac{1}{x}\right)$ has oscillatory discontinuity at point $x=0$.

Function $f\left(x\right)=\sin \left(\frac{1}{x}\right)$ has oscillatory discontinuity at point $x=0$.

Define the oscillatory discontinuity with one example.

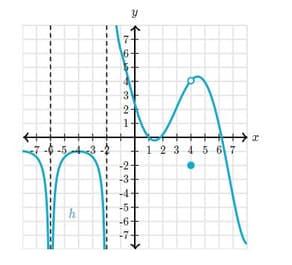
This is the graph of a function $h\left(x\right)$.

Find the $x$-value at which $h\left(x\right)$ has an isolated point discontinuity.